Les comparto una guía para que puedan entender PCA a fondo.
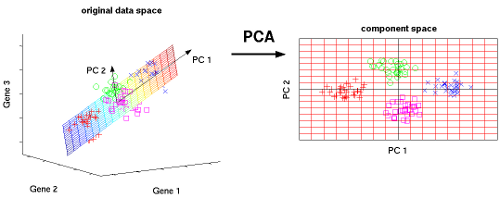
Análisis de componentes principales (PCA) es un método usado para la reducción de dimensionalidad de un conjunto de datos, preservando la varianza de los mismos. Desde un punto de vista de álgebra lineal PCA es un método de proyección de vectores sobre eigen-vectores.
Imagen tomada de: http://www.nlpca.org/pca_principal_component_analysis.html
0. Videos para entender la esencia general de PCA:
[1] STAT QUEST https://youtu.be/HMOI_lkzW08
[2] LUIS SERRANO https://www.youtube.com/watch?v=AniiwysJ-2Y
Para recordar la covarianza:
NOTA: PCA es SVD visto desde un punto de vista estadístico, por ello debe entenderse SVD
1. Conocimiento básicos de Álgebra Lineal,
Lo que deben prestar atención es que una multiplicación de una Matriz por un vector: Av = w.. Se debe entender como que: el vector v se sometió a la transformación A y se generó w.
Es importante que se entienda que el Determinante de una Matriz igualado a cero reduce la dimensionalidad. Este paso es FUNDAMENTAL para entender PCA, de hecho es la esencia de PCA.
Finalmente y siguiendo la idea anterior, se debe entender la noción de eigen-valor y eigen-vector...se relaciona con el determinante en cero.
2. Se sugiere el conocimiento del método SVD (Descomposición de Valores Singulares)
SVD es un método que usa los eigen-valores y eigen-vectores para representar a una matriz. Lo interesante de este método es que genera valores singulares, los cuales al multiplicarse forman matrices, las cuales al sumarse generan a la matriz original...Dichas matrices están ordenadas por la energía que aportan para la reconstrucción. Esta esencia se usa en PCA
El mejor video:
Cálculo SVD paso a paso
Interpretación geométrica
[6] https://youtu.be/LDYGTpSDlhI
Detalle técnico:
Dr. Strang
3. Entendiendo a detalle PCA
PCA es un método que usa una parte del método SVD y comparte la interpretación...las matrices generadas por los valores singulares ahora representan a los componentes principales.